Comparaison de suites
Il s'agit de comparer les vitesses de convergence ou de divergence des suites.
Définition :
Une suite
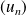 est négligeable devant une suite
est négligeable devant une suite
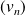 , s'il existe une suite
, s'il existe une suite
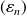 qui converge vers
qui converge vers
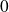 telle que :
telle que :
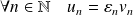 .
.
Notation :
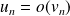 .
.
Si
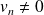 à partir d'un certain rang, alors
à partir d'un certain rang, alors
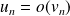 si et seulement si
si et seulement si
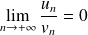 .
.
Fondamental :
Négligeabilités usuelles :
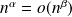 si
si
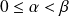 .
.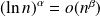 si
si
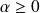 et
et
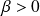 .
.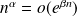 si
si
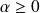 et
et
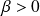 .
.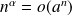 si
si
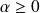 et
et
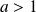 .
.
Fondamental :
Propriétés :
Si
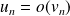 et si la suite
et si la suite
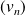 est convergente, alors la suite
est convergente, alors la suite
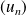 converge vers
converge vers
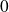 .
.Si
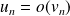 et
et
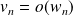 , alors
, alors
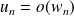 (transitivité).
(transitivité).Si
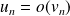 , alors
, alors
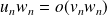 .
.Si
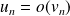 et
et
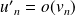 , alors
, alors
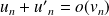 .
.Si
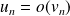 et
et
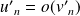 , alors
, alors
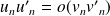 .
.Si
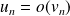 et
et
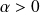 , alors
, alors
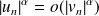 .
.
Attention :
La relation de négligeabilité n'est pas compatible avec la division (et donc avec les puissances négatives).
La relation de négligeabilité n'est pas compatible avec la composition.
Par exemple,
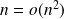 mais
mais
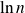 n'est pas négligeable devant
n'est pas négligeable devant
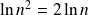 puisque le quotient est égal à
puisque le quotient est égal à
 .
.
Définition :
Une suite
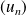 est équivalente à une suite
est équivalente à une suite
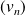 s'il existe une suite
s'il existe une suite
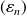 qui converge vers
qui converge vers
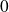 telle que :
telle que :
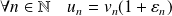 .
.
Notation :
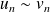 .
.
Si
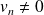 à partir d'un certain rang, alors
à partir d'un certain rang, alors
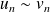 si et seulement si
si et seulement si
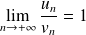 .
.
Si
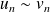 , alors les suites
, alors les suites
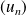 et
et
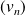 sont de même nature et admettent la même limite.
sont de même nature et admettent la même limite.
Fondamental :
Equivalences usuelles :
En
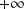 , un polynôme est équivalent à son terme de plus haut degré.
, un polynôme est équivalent à son terme de plus haut degré.En
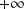 , une fraction rationnelle est équivalente au quotient des termes de plus haut degré de son numérateur et de son dénominateur.
, une fraction rationnelle est équivalente au quotient des termes de plus haut degré de son numérateur et de son dénominateur.Si
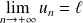 et si
et si
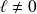 , alors
, alors
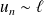 .
.Si
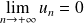 , alors :
, alors :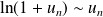 .
.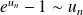 .
.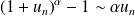 .
.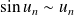 .
.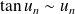 .
.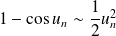 .
.
Si
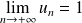 , alors :
, alors :
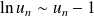 .
.
Fondamental :
Propriétés :
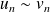 si et seulement si
si et seulement si
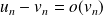 . On écrit
. On écrit
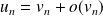 .
.Si
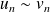 , alors
, alors
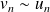 (symétrie).
(symétrie).Si
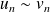 et
et
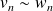 , alors
, alors
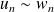 (transitivité).
(transitivité).Si
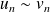 , alors
, alors
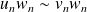 .
.Si
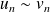 et
et
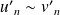 , alors
, alors
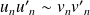 .
.Si
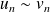 et
et
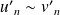 , alors
, alors
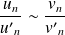 .
.Si
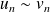 , alors
, alors
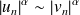 .
.
Attention :
La relation d'équivalence n'est pas compatible avec l'addition.
La relation d'équivalence n'est pas compatible avec la composition.
Par exemple,
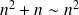 , mais les suites de termes généraux
, mais les suites de termes généraux
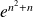 et
et
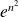 ne sont pas équivalentes puisque le quotient
ne sont pas équivalentes puisque le quotient
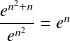 ne tend pas vers
ne tend pas vers
 .
.
Définition :
Une suite
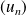 est dominée par une suite
est dominée par une suite
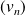 s'il existe une suite
s'il existe une suite
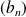 bornée telle que :
bornée telle que :
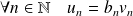 .
.
Notation :
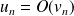 .
.
Si
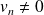 à partir d'un certain rang, alors
à partir d'un certain rang, alors
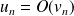 si et seulement si la suite
si et seulement si la suite
 est bornée.
est bornée.
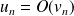 si et seulement si il existe un réel
si et seulement si il existe un réel
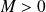 tel que :
tel que :
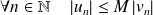 .
.
Attention !
La suite
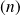 est dominée par la suite
est dominée par la suite
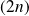 , mais aussi par la suite
, mais aussi par la suite
 .
.
Donc
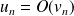 ne prouve pas que
ne prouve pas que
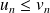 (ni l'inverse).
(ni l'inverse).





