Suites usuelles
Définition :
Une suite
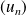 est arithmétique s'il existe un réel
est arithmétique s'il existe un réel
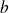 (appelé raison de la suite) tel que :
(appelé raison de la suite) tel que :
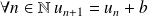 .
.
Fondamental :
Propriétés :
Son terme général est :
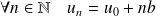 .
.Pour tous les entiers
 et
et
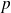 :
:
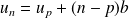 .
.Pour tous les entiers
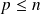 :
:
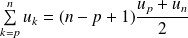 .
.
Définition :
Une suite
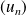 est géométrique s'il existe un réel
est géométrique s'il existe un réel
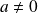 (appelé raison de la suite) tel que :
(appelé raison de la suite) tel que :
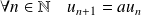 .
.
Fondamental :
Propriétés :
Son terme général est :
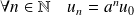 .
.Pour tous les entiers
 et
et
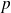 :
:
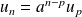 .
.Pour tous les entiers
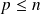 :
:
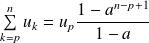 si
si
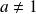 , et
, et
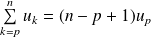 si
si
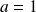 .
.
Définition :
Une suite
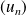 est arithmético-géométrique s'il existe des réels
est arithmético-géométrique s'il existe des réels
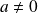 et
et
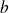 tels que :
tels que :
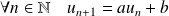 .
.
Méthode :
Calcul du terme général :
Si
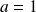 , la suite est arithmétique.
, la suite est arithmétique.Si
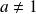 , il existe un unique réel
, il existe un unique réel
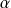 (point fixe) tel que
(point fixe) tel que
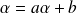 .
.Alors, la suite de terme général
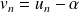 est géométrique de raison
est géométrique de raison
 .
. On en déduit
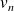 , puis
, puis
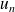 en fonction de
en fonction de
 .
.
Définition :
Une suite
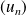 suit une relation de récurrence linéaire d'ordre 2 s'il existe deux réels
suit une relation de récurrence linéaire d'ordre 2 s'il existe deux réels
 et
et
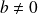 tels que :
tels que :
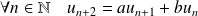 .
.
Méthode :
Calcul du terme général :
L'équation
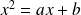 est appelée équation caractéristique associée à la relation de récurrence.
est appelée équation caractéristique associée à la relation de récurrence.Son discriminant est
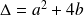 .
.
Premier cas :
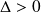 .
.L'équation caractéristique possède deux racines distinctes
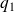 et
et
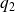 .
.Alors il existe deux réels
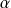 et
et
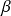 tels que :
tels que :
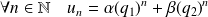 .
.
Deuxième cas :
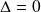 .
.L'équation caractéristique possède une racine double
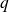 .
.Alors il existe deux réels
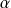 et
et
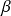 tels que :
tels que :
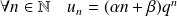 .
.
Troisième cas :
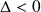 .
.L'équation caractéristique possède deux racines complexes conjuguées que l'on met sous forme trigonométrique :
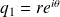 et
et
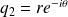 .
.Alors il existe deux réels
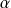 et
et
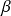 tels que :
tels que :
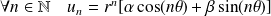 .
.
Dans les trois cas, on détermine les réels
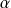 et
et
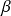 à l'aide des conditions initiales.
à l'aide des conditions initiales.





