Exo 1
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
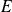un plan vectoriel euclidien orienté.
Soit
une rotation du plan et
une réflexion du plan.
Question
Comparer les matrices de la rotation
dans deux bases orthonormales de même sens.
La matrice de passage est une matrice de rotation.
Soient
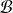et
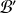deux bases orthonormales de même sens.
La matrice
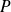de passage de
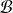à
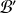est donc une matrice orthogonale avec
.
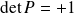Donc il existe un réel
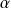tel que :
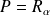. Donc :
.
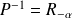Dans la base
, la rotation
a une matrice
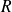orthogonale et
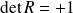. Donc il existe un réel
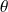tel que :
.
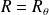Dans la base
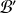, la matrice de
est :
.
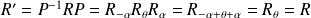Conclusion : La rotation
a la même matrice dans deux bases orthonormales de même sens.
Question
Comparer les matrices de la rotation
dans deux bases orthonormales de sens contraires.
La matrice de passage est une matrice de réflexion.
Soient
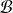et
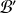deux bases orthonormales de sens contraires.
Ici, la matrice
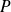de passage de
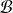à
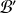est une matrice orthogonale avec
.
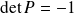Donc il existe un réel
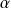tel que :
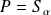. Donc :
.
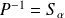Dans la base
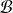, la rotation
a une matrice
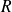orthogonale et
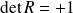. Donc il existe un réel
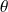tel que :
.
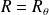Dans la base
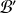, la matrice de
est :
.
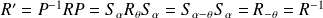Conclusion : La rotation
a deux matrices inverses l'une de l'autre dans deux bases orthonormales de sens contraires.
Question
Comparer les matrices de la réflexion
dans deux bases orthonormales de même sens.
Soient
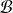et
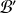deux bases orthonormales de même sens.
La matrice
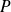de passage de
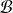à
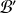est donc une matrice orthogonale avec
.
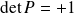Donc il existe un réel
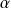tel que :
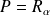. Donc :
.
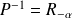Dans la base
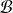, la réflexion
a une matrice
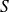orthogonale et
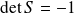. Donc il existe un réel
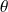tel que :
.
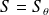Dans la base
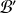, la matrice de
est :
.
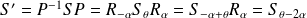Conclusion : La réflexion
n'a pas la même matrice dans deux bases orthonormales de même sens.
Question
Comparer les matrices de la réflexion
dans deux bases orthonormales de sens contraires.
Soient
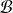et
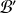deux bases orthonormales de sens contraires.
Ici, la matrice
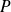de passage de
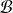à
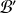est une matrice orthogonale avec
.
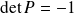Donc il existe un réel
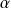tel que :
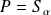. Donc :
.
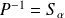Dans la base
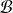, la réflexion
a une matrice
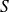orthogonale et
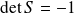. Donc il existe un réel
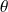tel que :
.
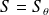Dans la base
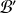, la matrice de
est :
.
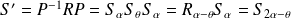Conclusion : La réflexion
n'a pas non plus la même matrice dans deux bases orthonormales de sens contraires.
