Déterminant de n vecteurs
Définition :
Soit
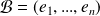une base d'un espace vectoriel
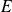et
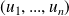une famille de vecteurs définie par :
.
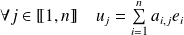Le déterminant de
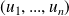dans la base
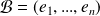est :
.
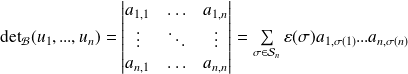Le rang du déterminant est le rang de
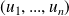, donc la dimension de
.
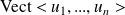Exemple :
Calculez le déterminant
.
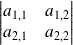Fondamental :
Propriétés :
L'application
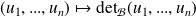est une forme multilinéaire alternée, c'est-à-dire linéaire par rapport à chaque vecteur, et changée en son opposée si l'on intervertit deux vecteurs.La famille
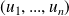est liée si et seulement si
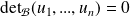.La famille
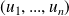est une base si et seulement si
.
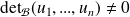Fondamental :
Conséquences :
Si une ligne ou une colonne est combinaison linéaire des autres, le déterminant est nul.
On ne change pas un déterminant en ajoutant à une ligne ou à une colonne une combinaison linéaire des autres.
Si l'on multiplie une ligne ou une colonne par un scalaire
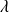, le déterminant est multiplié par
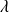.Si l'on intervertit deux lignes ou deux colonnes, le déterminant est multiplié par
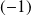.On ne change pas un déterminant en intervertissant les lignes et les colonnes (Transposition).
