Racines d'un polynôme
Définition :
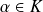est racine du polynôme
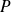si
.
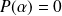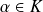est racine du polynôme
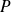si et seulement si
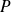est divisible par
.
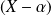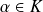est racine d'ordre
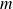de
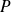si
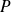est divisible par
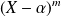et pas par
.
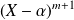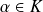est racine d'ordre
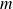de
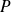si et seulement si
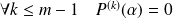et
.
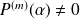Fondamental :
Conséquence :
Un polynôme de degré
admet au plus
racines. Si un polynôme de degré inférieur ou égal à
admet
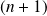racines, c'est le polynôme nul.
Fondamental :
Théorème de D'Alembert-Gauss : Tout polynôme de
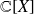admet au moins une racine dans
.
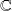Conséquence :
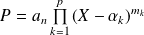si
, ...,
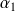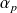sont les racines complexes de
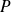avec leur ordre de multiplicité
, ...,
.
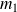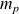Définition :
Un polynôme
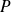est scindé si :
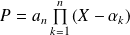où
, ...,
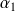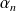sont les racines de
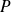avec leur ordre de multiplicité.
Fonctions symétriques élémentaires :
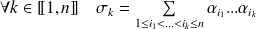si
, ...,
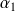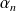sont les racines de
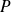avec leur ordre de multiplicité.
Relations avec les coefficients :
.
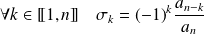