Vocabulaire des applications
Définition :
Etant donnés deux ensembles non vides
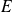 et
et
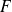 , et
, et
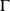 une partie non vide de
une partie non vide de
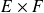 , on définit une relation binaire
, on définit une relation binaire
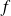 par :
par :
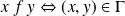 .
.
Cette relation binaire est :
une application de
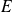 vers
vers
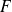 si, pour tout
si, pour tout
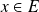 , il existe un unique
, il existe un unique
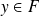 tel que
tel que
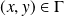 . On le note
. On le note
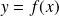 .
.Si
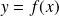 , l'élément
, l'élément
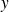 de
de
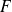 est l'image de
est l'image de
 par
par
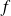 , et l'élément
, et l'élément
 de
de
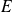 est un antécédent de
est un antécédent de
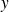 (il n'est pas toujours unique).
(il n'est pas toujours unique).une fonction de
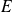 vers
vers
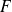 si, pour tout
si, pour tout
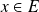 , il existe au plus un
, il existe au plus un
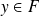 tel que
tel que
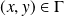 . S'il existe, on le note
. S'il existe, on le note
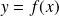 .
. L'ensemble des éléments
 qui ont une image par la fonction
qui ont une image par la fonction
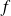 est l'ensemble de définition de la fonction souvent noté
est l'ensemble de définition de la fonction souvent noté
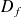 .
.
Définition :
Soit
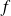 est une application de
est une application de
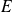 dans
dans
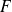 .
.
• Si
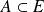 , la restriction de
, la restriction de
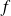 à
à
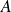 est l'application notée
est l'application notée
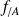 de
de
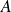 vers
vers
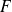 qui coïncide avec
qui coïncide avec
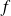 pour tout élément de
pour tout élément de
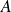 :
:
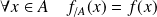 .
.
• Si
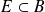 , un prolongement de
, un prolongement de
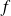 à
à
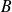 est une application
est une application
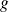 de
de
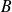 vers
vers
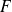 telle que
telle que
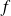 soit la restriction de
soit la restriction de
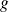 à
à
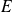 :
:
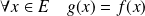 .
.
La restriction est unique, mais pas le prolongement.
La restriction d'une fonction à son ensemble de définition est une application.
Définition :
Si
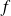 est une application de
est une application de
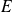 dans
dans
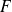 et
et
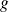 une application de
une application de
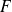 dans
dans
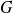 , on appelle composée de
, on appelle composée de
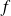 par
par
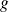 l'application de
l'application de
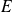 dans
dans
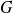 définie par :
définie par :
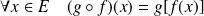 .
.
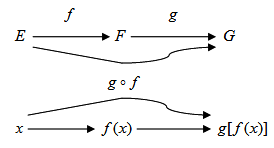
Fondamental :
Propriétés :
La composition des applications est associative :
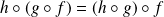 .
.La composition des applications n'est pas commutative.





