Parties d'un ensemble
Définition :
Un ensemble
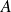est une partie d'un ensemble
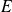si :
.
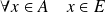A toute partie
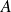de
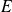on peut associer une propriété notée
:
.
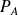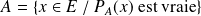C'est ce que l'on fait, par exemple, quand on résout une équation ou une inéquation :
.
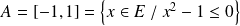Fondamental :
Les parties d'un ensemble
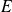forment un ensemble noté
.
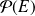Il est muni :
d'une relation d'ordre partiel (inclusion) :
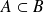si et seulement si
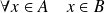. d'une relation d'équivalence (égalité) :
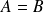si et seulement si
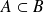et
.
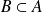Si les parties
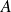et
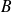sont associées à des propriétés
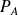et
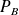, alors :
-
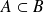si et seulement si
. -
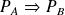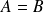si et seulement si
.
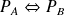Méthode :
Pour démontrer l'égalité de deux ensembles
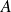et
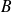, on raisonne en deux étapes :
On prend un élément quelconque de
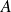et l'on démontre qu'il appartient à
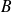.On prend un élément quelconque de
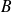et l'on démontre qu'il appartient à
.
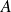