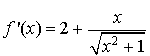
En réduisant au même dénominateur :
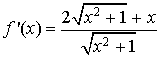
Pour tout
 , on a :
, on a :
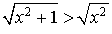
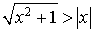
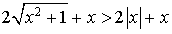
Or 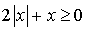 .
.
En effet :
pour 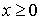 ,
, 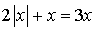 , et
, et 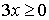 ,
,
pour 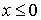 ,
, 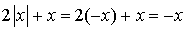 , et
, et 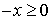 .
.
On peut aussi justifier :
pour 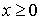 ,
, 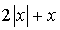 est la somme de deux nombres positifs,
est la somme de deux nombres positifs,
pour 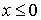 ,
, 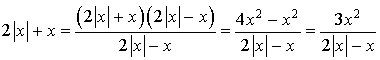 , et
, et 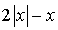 est la somme de deux nombres positifs, donc
est la somme de deux nombres positifs, donc 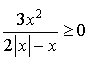 .
.
Donc 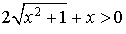 , ce qui montre que
, ce qui montre que
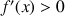 et par conséquent que
et par conséquent que
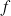 est strictement croissante sur R.
est strictement croissante sur R.