Enoncé
L'espace est rapporté au repère orthonormal ![]() .
.
Soit
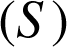 la surface d'équation
la surface d'équation ![]() .
.
Répondre par vrai ou faux aux affirmations proposées.
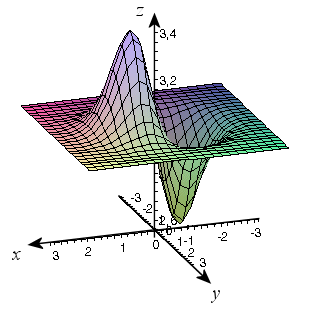
4) Aucun point de
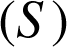 n'a une côte égale à
n'a une côte égale à
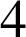 .
.
Résultat
Correction
Explications
Le point ![]() de
de
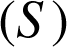 a une cote égale à
a une cote égale à
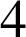 si et seulement si
si et seulement si ![]() et
et
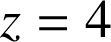 c'est-à-dire :
c'est-à-dire : ![]() . La fonction exponentielle ne prenant que des valeurs strictement positives, on peut supposer
. La fonction exponentielle ne prenant que des valeurs strictement positives, on peut supposer
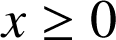 .
.
Soit
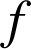 la fonction définie sur
la fonction définie sur
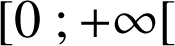 par
par ![]() ; étudions ses variations.
; étudions ses variations.
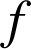 est le produit de fonctions dérivables sur
est le produit de fonctions dérivables sur
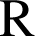 donc est dérivable sur
donc est dérivable sur
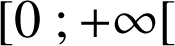 et
et
![]() .
.
![]() est du signe de
est du signe de ![]() qui est un trinôme dont les racines sont
qui est un trinôme dont les racines sont ![]() et
et ![]() .
.
Donc
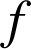 est croissante sur
est croissante sur 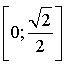 et décroissante sur
et décroissante sur 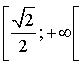 et
et 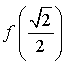 est le maximum de
est le maximum de
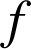 sur
sur
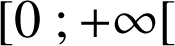 . Or
. Or 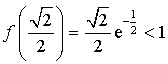 donc, pour tout
donc, pour tout
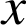 dans
dans
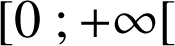 , on a
, on a ![]() et pour tout réel
et pour tout réel
 :
: ![]() et donc
et donc ![]() .
.
L'équation ![]() n'a pas de solution.
n'a pas de solution.