Enoncé
6) La droite
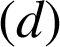 passant par
passant par ![]() , de vecteur normal
, de vecteur normal ![]() est tangente au cercle
est tangente au cercle ![]() de diamètre
de diamètre
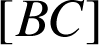 où
où ![]() et
et ![]() .
.
Résultat
Correction
Explications
La droite
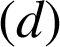 est l'ensemble des points
est l'ensemble des points ![]() tels que
tels que ![]() .
.
![]()
Une équation de
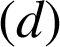 est :
est : ![]() .
.
Le cercle ![]() est l'ensemble des points
est l'ensemble des points ![]() tels que
tels que ![]() .
.
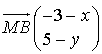 et
et 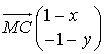 donc :
donc :
Une équation de ![]() est
est ![]() .
.
Les couples de coordonnées ![]() des points d'intersection de
des points d'intersection de ![]() et
et
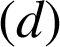 sont solutions du système :
sont solutions du système :
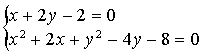
qui équivaut à 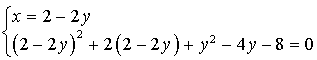
ou encore :
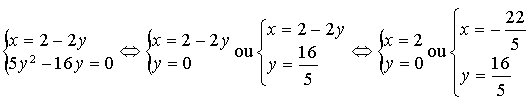
![]() et
et
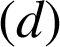 ont deux points d'intersection donc
ont deux points d'intersection donc
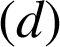 n'est pas tangente à
n'est pas tangente à ![]() .
.
Autre façon :
Le rayon de ![]() est
est 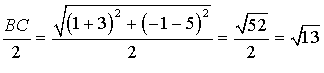 .
.
![]() , milieu de
, milieu de
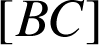 , est le centre de
, est le centre de ![]() ; la distance de
; la distance de
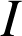 à la droite
à la droite
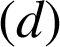 est :
est : 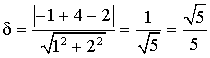 . Comme
. Comme 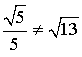 ,
,
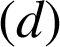 n'est pas tangente à
n'est pas tangente à ![]() .
.