Enoncé
1) Soient
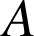et
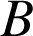deux points distincts et différents de
. Si
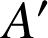et
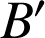sont les images de
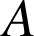et
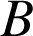par une similitude directe de centre
, alors
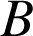et
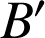sont les images de
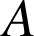et
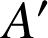par une similitude directe de centre
.
Résultat
Correction
Explications
Soient
,
,
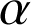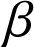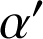et
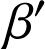les affixes de
,
,
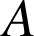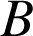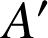et
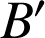. Il existe un nombre complexe
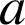, non nul, tel que
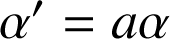et
.
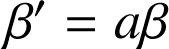Comme
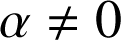et
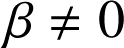, on a 
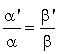, et donc 
.
En posant 
, on a 
et 
, ce qui montre que les points
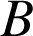et
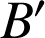sont les images de
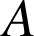et
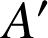par la similitude de centre
qui a pour écriture complexe 
.