Enoncé
6) Étant donnés deux triangles équilatéraux directs
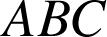 et
et
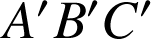 , il existe une similitude directe et une seule qui transforme
, il existe une similitude directe et une seule qui transforme
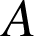 en
en
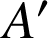 ,
,
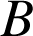 en
en
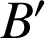 et
et
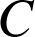 en
en
 .
.
Résultat
Correction
Explications
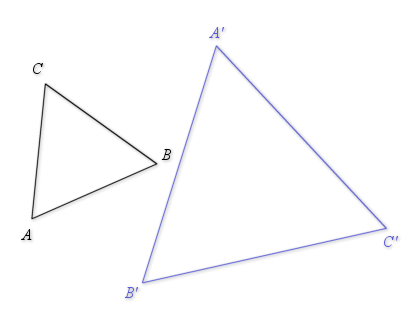
Puisque
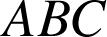 et
et
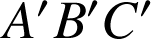 sont des triangles,
sont des triangles,
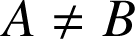 et
et
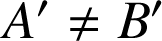 . D'après le cours, il existe une similitude directe
. D'après le cours, il existe une similitude directe
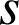 , unique, transformant
, unique, transformant
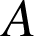 en
en
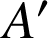 et
et
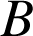 en
en
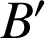 .
.
Appelons
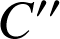 l'image de
l'image de
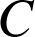 par
par
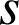 .
.
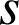 conserve les angles orienté donc :
conserve les angles orienté donc :
![]() et
et ![]()
Le triangle
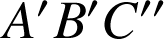 est donc un triangle équilatéral direct. On a donc
est donc un triangle équilatéral direct. On a donc
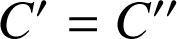 .
.
Au final ![]() ,
, ![]() et
et ![]() .
.