Enoncé
3) On considère l'application
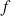 qui au point
qui au point
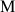 d'affixe
d'affixe
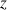 associe le point
associe le point
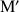 d'affixe
d'affixe
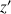 avec
avec ![]() .
.
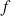 est une homothétie.
est une homothétie.
Résultat
Correction
Explications
En effet, en résolvant l'équation
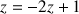 , on peut justifier que
, on peut justifier que
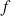 a un point invariant unique d'affixe
a un point invariant unique d'affixe ![]() .
.
On peut écrire :
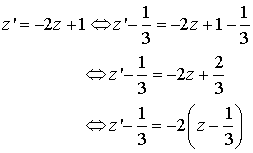
L'application
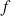 a donc une écriture complexe de la forme
a donc une écriture complexe de la forme ![]() avec
avec ![]() et
et ![]() .
.
Donc
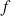 est une homothétie de centre
est une homothétie de centre
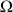 d'affixe
d'affixe
 et de rapport
et de rapport
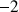 .
.