Enoncé
5) En accolant 6 carrés identiques, on peut former 2 rectangles, un rectangle de 1 sur 6, et un rectangle de 2 sur 3. En accolant 200 carrés identiques, combien peut-on former de rectangles (sans trou) différents ?
Résultat
Correction
Explications
On cherche le nombre de paires d'entiers naturels dont le produit est
.
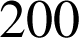donc
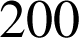admet 12 diviseurs. Il est donc possible de former 6 rectangles (dimensions : 
, 
, 
, 
, 
, 
).