La surface
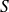 est caractérisée par ses équations paramétriques :
est caractérisée par ses équations paramétriques :
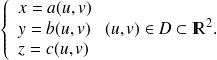
On suppose que les fonctions
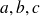 sont différentiables en
sont différentiables en
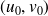 , la surface est alors dite différentiable en
, la surface est alors dite différentiable en
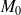 .
.
Si la surface
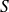 est différentiable en
est différentiable en
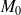 , si les vecteurs
, si les vecteurs
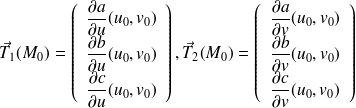
ne sont pas colinéaires, il existe un plan
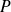 tangent à
tangent à
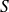 en
en
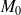 .
.
Ce plan contient
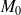 et les vecteurs
et les vecteurs
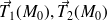 .
.
Si les composantes de
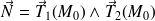 sont
sont
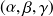 , l'équation de
, l'équation de
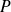 est
est
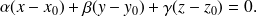
Le plan tangent à une surface
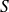 en
en
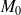 s'il existe, est un plan qui contient les droites tangentes à toutes les courbes tracées sur
s'il existe, est un plan qui contient les droites tangentes à toutes les courbes tracées sur
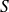 et passant par
et passant par
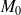 . Admettons que, sous les hypothèses du théorème, ce plan tangent existe, il suffit maintenant de 2 vecteurs pour le caractériser.
. Admettons que, sous les hypothèses du théorème, ce plan tangent existe, il suffit maintenant de 2 vecteurs pour le caractériser.
On définit les courbes
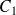 et
et
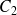 paramétrées par :
paramétrées par :
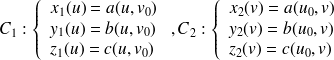
Ces courbes sont tracées sur la surface
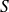 et elles passent par
et elles passent par
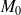 . Un vecteur tangent à
. Un vecteur tangent à
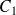 en
en
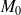 est le vecteur de composantes
est le vecteur de composantes
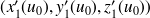 , or ce vecteur est le vecteur
, or ce vecteur est le vecteur
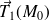 . De même un vecteur tangent \`a
. De même un vecteur tangent \`a
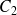 en
en
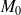 est le vecteur
est le vecteur
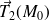 . Donc les vecteurs
. Donc les vecteurs
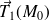 et
et
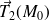 sont deux vecteurs non colinéaires du plan tangent, ce qui définit complétement ce plan
sont deux vecteurs non colinéaires du plan tangent, ce qui définit complétement ce plan