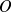Une surface est dite de révolution autour d'un axe
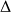si son intersection avec un plan quelconque perpendiculaire à
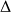est vide ou constituée d'un ou plusieurs cercles centrés sur
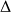(un cercle peut être réduit à un point).
Citons par exemple les sphères, les cônes, les cylindres, les tores. Nous allons retrouver ces surfaces et quelques autres maintenant.
L'étude d'une surface
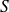de révolution se fait en 2 étapes :
-
On détecte que la surface est de révolution autour de
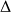en étudiant l'intersection de
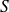avec un plan quelconque perpendiculaire à
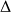, on doit trouver l'ensemble vide, ou un (ou plusieurs) cercle(s) centré(s) sur
. -
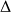On détermine la nature de
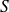en étudiant la courbe intersection de
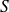avec un plan particulier contenant
.
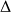Par exemple, étudions la surface
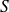qui a pour équation
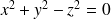. Cette surface est une quadrique.
-
L'intersection de
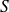avec un plan quelconque perpendiculaire à
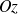d'équation
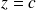, est un cercle situé dans le plan
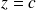, de centre
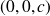et de rayon
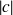. Donc la surface est de révolution autour de
. -
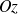On détermine l'intersection de
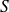avec un plan particulier contenant
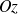: le plan
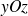par exemple, on a donc
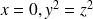. On obtient ainsi 2 droites du plan
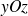qui ont pour équation
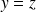et
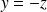. Donc la surface
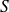est un cône d'axe
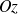et de sommet
