Rappelons l'équation cartésienne de quelques surfaces connues :

• Si 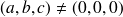, 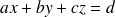est l'équation d'un plan dont un vecteur normal est le vecteur

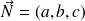
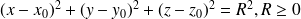• est l'équation d'une sphére de centre 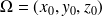et de rayon 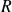. En effet l'équation précédente traduit la propriété : "la distance du point 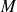de coordonnées 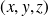au point 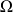est constante et égale à 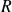", ce qui est bien la propriété caractéristique d'une sphére.

• Dans l'espace 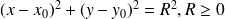est l'équation d'un cylindre de révolution de rayon 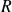, dont l'axe 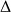a pour équations 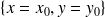. En effet on a la propriété : "la distance du point 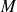de coordonnées 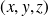à l'axe 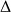est constante et égale à 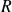", ce qui est bien la propriété caractéristique d'un cylindre.

  Bien sûr, si le contexte indique que l'on se trouve dans le plan 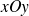, l'équation

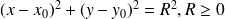  est l'équation d'un cercle.

• Les quadriques sont des surfaces dont l'équation cartésienne est obtenue à partir d'un polynôme de degré 2 (les variables sont 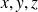). On retrouve dans cette famille les surfaces classiques : sphères, cylindres, cônes et les surfaces un peu moins classiques : paraboloïdes, hyperboloïdes, ellipsoïdes. (Voir les figures qui suivent et celles qui se trouvent dans le document référencé.) Pour l'étude de certaines de ces surfaces voir le paragraphe de cours référencé.

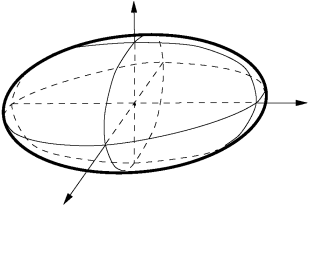
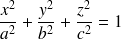
ellipsoïde

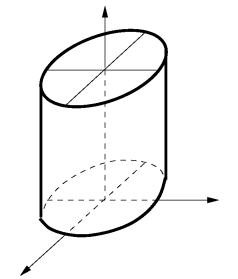
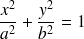
cylindre

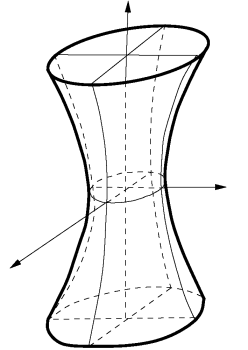
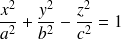
hyperboloïde à une nappe

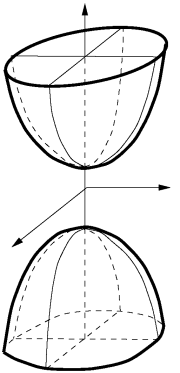
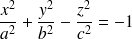
hyperboloïde à 2 nappes

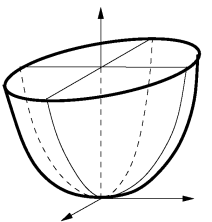
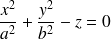
paraboloïde

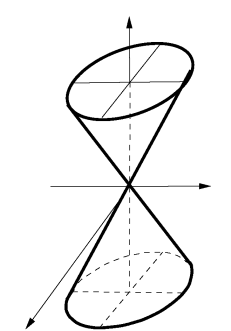
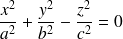
cône