Etude des courbes paramétrées du plan

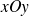
On veut étudier et représenter graphiquement une courbe du plan 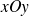dont les équations paramétriques sont : .

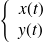L'étude se décompose en plusieurs étapes :

1. Etude des domaines de définition des fonction et 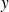: la courbe est alors définie sur l'intersection de ces 2 domaines.

2. Etude des symétries éventuelles :

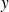   • Si la fonction est paire et la fonction est impaire, la courbe est symétrique par rapport à l'axe 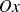. On limite donc l'étude à l'intervalle 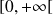, puis on effectue la symétrie.

   • Si la fonction est impaire et la fonction 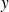est paire, la courbe est symétrique par rapport à l'axe 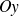. On limite donc l'étude à l'intervalle 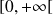, puis on effectue la symétrie.

   • Si la fonction est paire et la fonction 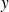est paire, l'étude sur l'intervalle 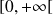permet d'obtenir toute la courbe.

   • Si la fonction est impaire et la fonction 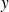est impaire, la courbe est symétrique par rapport à 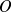. On limite donc l'étude à l'intervalle 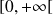, puis on effectue la symétrie.

   Pour illustrer les propriétés précédentes faites une figure sur laquelle vous représenterez les points 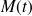et 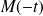dans chacun des cas cités.

3. Etude des variations : Si les fonctions et 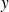sont dérivables, on calcule leurs dérivées. On dresse un tableau de variation où figurent les signes de 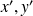et les variations de 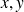en fonction de .

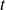4. Etude des branches infinies : si lorsque 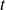tend vers 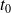(ou vers l'infini), ou 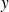tend vers l'infini, on a une branche infinie. Plusieurs cas peuvent se présenter :

   • Lorsque 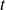tend vers 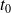(ou vers l'infini), tend vers l'infini et 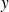tend vers 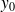. On a alors une asymptote horizontale d'équation 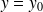. La position de la courbe par rapport à l'asymptote se déduit immédiatement du tableau de variation.

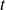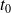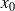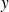   • Lorsque tend vers (ou vers l'infini), tend vers et tend vers l'infini. On a alors une asymptote verticale d'équation 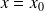. La position de la courbe par rapport à l'asymptote se déduit immédiatement du tableau de variation.

   • Lorsque 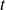tend vers 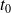(ou vers l'infini), tend vers l'infini et 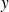tend vers l'infini. Il n'est pas possible alors de conclure immédiatement. On doit effectuer une étude supplémentaire :

     • Si 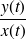tend vers l'infini, on est dans le cas d'une branche parabolique d'axe 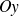ou, ce qui est équivalent, d'une direction asymptotique d'axe .

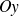     • Si 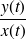tend vers 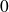, on est dans le cas d'une branche parabolique d'axe 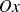ou, ce qui est équivalent, d'une direction asymptotique d'axe .

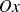     • Si 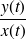tend vers réel non nul, on effectue une étude supplémentaire :

       • Si 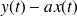tend vers l'infini et si on appelle 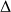la droite d'équation 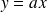, on est dans le cas d'une branche parabolique d'axe 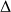ou, ce qui est équivalent, d'une direction asymptotique d'axe .

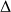       • Si 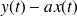tend vers 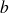, on a une asymptote d'équation 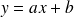. Cette fois-ci la position de la courbe par rapport à l'asymptote n'est plus immédiate, il faut étudier le signe de .

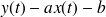5. Tracé de la courbe : on utilise toutes les informations recueillies précédemment. On peut également tracer les vecteurs tangents en certains points remarquables.