Tangente à une courbe du plan 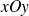définie par une équation explicite

Soit 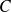une courbe du plan 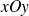dont l'équation explicite est

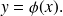
On suppose que 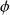est dérivable. Soit 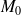un point de .

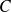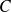On sait que l'équation de la droite tangente à au poin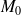t est :

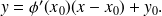
On peut redémontrer ce résultat :

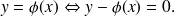
Si l'on note

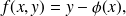
on a

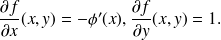
On utilise le résultat 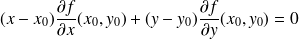et on obtient l'équation de la droite tangente.

On aurait pu également utiliser les propriétés de la dérivée vues dans le chapitre "fonctions d'une variable réelle".

On sait que 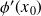est la pente de , tangente à 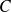au point 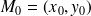. On peut donc écrire