Vecteur tangent à une courbe paramétrée du plan
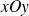
Soit la courbe
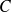dont les équations paramétriques sont :
.
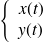On veut étudier cette courbe localement au voisinage du point
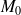. On rappelle que la droite tangente à
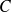en
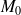est la position limite de la droite de vecteur directeur
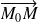quand
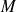tend vers
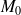sur
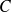. Or
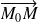a pour composantes
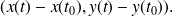
Ce vecteur est colinéaire au vecteur
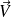de composantes
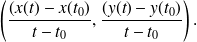
La limite du vecteur
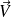quand
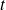tend vers
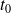est donc le vecteur
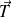de composantes
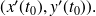
Soit
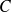la courbe dont les équations paramétriques sont :
,
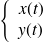le vecteur
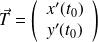, s'il n'est pas nul, est tangent en
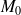à la courbe
.
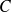Par exemple le cercle du plan
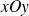de centre
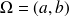et de rayon
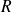a pour équations paramétriques :
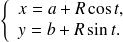
Un vecteur tangent
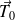en
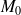a pour composantes
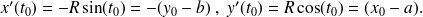
On retrouve la propriété bien connue :
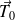est orthogonal à
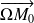. Il suffit d'effectuer le produit scalaire pour s'en convaincre.