Une droite
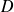dans l'espace
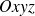peut être définie de plusieurs façons :
-
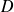est définie par un point
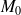de coordonnées
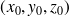et un vecteur directeur (non nul)
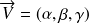. On a alors :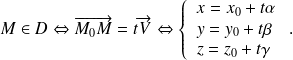
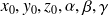sont des constantes caractéristiques de
,
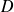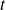est le paramètre qui varie quans le point
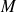décrit
. -
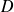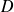est définie comme intersection de deux plans non parallèles
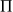et
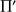d'équations cartésiennes :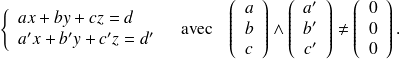 
On obtient naturellement les équations cartésiennes de
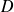. Ces équations ne sont pas uniques, une droite est intersection d'une infinité de plans, il suffit de choisir les équations de deux d'entre eux.Attention, dans l'espace
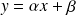n'est pas l'équation d'une droite, c'est l'équation d'un plan. De même
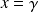est l'équation d'un plan.
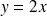dans l'espace est l'équation d'un plan.
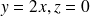sont les équations d'une droite qui appartient au plan précédent.
Soit
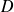la droite passant par le point
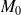et de vecteur directeur (non nul)
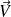. La distance d'un point
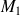à
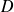vaut
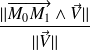
La proposition précédente est à démontrer en exercice.