Proposition
Soit
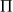le plan d'équation
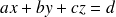, soit
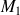, un point de coordonnées
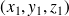, la distance de
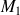à
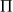est égale à
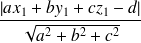
Lorsque
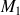appartient au plan
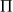, ses coordonnées vérifient l'équation du plan et on retrouve bien sûr que la distance de
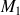au plan est nulle.
Proposition
Soit
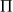le plan d'équation
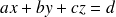, soit
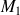, un point de coordonnées
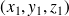, on note
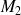le point projection orthogonale de
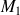sur
.
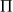Les coordonnées de
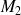sont données par les relations :
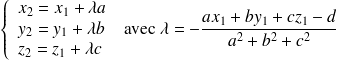
En utilisant la proposition précédente on retrouve la distance de
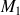au plan
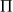, il suffit de calculer la norme de
.
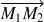