Dans tout ce qui suit l'espace est muni d'un repère orthonormé

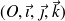
Un plan dans l'espace peut être défini de plusieurs façons :

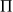1. est défini par un point 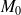de coordonnées 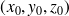et un vecteur normal (non nul) 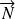de composantes .

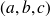   On a donc

   

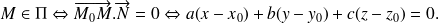
   On obtient une équation cartésienne de .

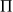   Si on pose 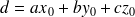, on retrouve l'équation cartésienne générale d'un

   plan (revoir l'exercice de cours 1):

   

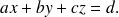
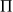2. est défini par un point 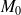de coordonnées 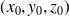et deux vecteurs du plan non colinéaires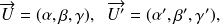

   

   On a donc :

   

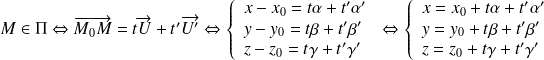
   On obtient ainsi des équations paramétriques du plan , sont des constantes caractéristiques du plan , 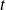et 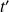sont les deux paramètres qui varient quand le point 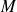décrit le plan.

   On aurait pu également obtenir une équation cartésienne de 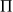en se ramenant au cas \ref {un}. Il suffisait de choisir .

   

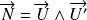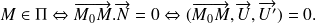
   Revoir le produit mixte, on traduit alors que les trois vecteurs 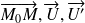sont coplanaires.

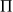3. est défini par trois points non alignés .

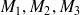   On peut se ramener au cas \ref{un} en choisissant par exemple

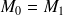   et ,

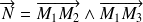   on traduit alors que les vecteurs 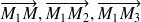sont coplanaires. On obtient une équation cartésienne de 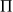( revoir l'exercice \polyref {C2-2-7}).

   On peut se ramener au cas \ref{deux} en choisissant par exemple

   , ,

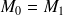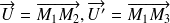   on obtiendrait des équations paramétriques de .
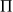