Intersection de droites du plan
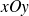
Pour étudier l'intersection de deux droites
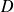 et
et
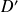 d'équations respectives
d'équations respectives
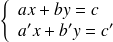
il suffit de résoudre le système de deux équations
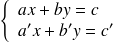 , ce système a une solution unique si et seulement si
, ce système a une solution unique si et seulement si
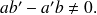
La solution unique donne alors les coordonnées de l'unique point d'intersection de
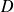 et
et
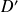 .
.
Si
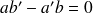 , les vecteurs directeurs
, les vecteurs directeurs
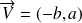 et
et
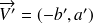 sont colinéaires. On peut utiliser le produit vectoriel pour le vérifier, les vecteurs
sont colinéaires. On peut utiliser le produit vectoriel pour le vérifier, les vecteurs
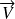 et
et
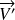 sont dans le plan
sont dans le plan
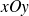 , leur troisième composante est donc nulle, le produit vectoriel (orthogonal à
, leur troisième composante est donc nulle, le produit vectoriel (orthogonal à
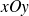 ) a alors pour composantes
) a alors pour composantes
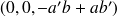 .
.
Lorsque
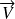 et
et
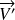 sont colinéaires, deux cas sont possibles pour les droites
sont colinéaires, deux cas sont possibles pour les droites
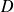 et
et
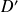 :
:
-
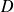 et
et
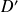 sont confondues, le système ( \ref{DD'}) admet une infinité de solutions.
sont confondues, le système ( \ref{DD'}) admet une infinité de solutions. -
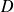 et
et
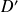 sont parallèles non confondues le système ( \ref{DD'}) n'admet pas de solution.
sont parallèles non confondues le système ( \ref{DD'}) n'admet pas de solution.