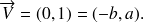Équation cartésienne des droites du plan

Dans tout ce qui suit le plan est muni d'un repère orthonormé

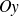Les droites du plan non parallèles à l'axe ont pour équation

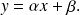
Les droites du plan 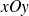parallèles à l'axe 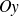ont pour équation

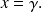
Une façon de regrouper les deux cas précédents est d'écrire l'équation des droites du plan sous la forme

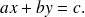
Les coefficients 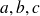sont définis à une constante multiplicative près.

Pour les droites non parallèles à 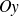on peut choisir par exemple :

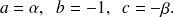
Pour les droites parallèles à on peut choisir par exemple :

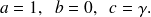
Un vecteur directeur de la droite d'équation 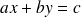est .

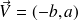On peut démontrer ce résultat dans le cas des droites non parallèles à l'axe . Choisissons deux points particuliers sur la droite d'équation .

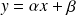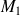de coordonnées 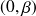et 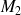de coordonnées 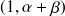, on obtient un vecteur directeur de :

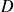Dans le cas des droites parallèles à , un vecteur directeur est