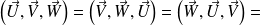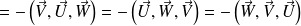Soient
,
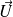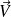et
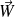trois vecteurs de
.
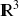Le produit mixte de
,
,
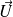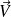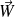est le scalaire défini par :
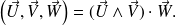
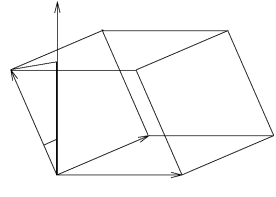
On démontre facilement que la valeur absolue du produit mixte est égale au volume du parallélépipède construit sur
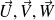. En effet ce volume est égal à l'aire d'une base multipliée par la hauteur correspondante :
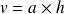
On utilise les propriétés du produit vectoriel. L'aire
de la base construite sur
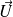et
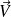vaut
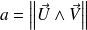. La hauteur
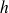vaut
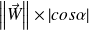, où
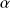est l'angle entre
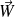et un vecteur normal à la base, on peut choisir comme vecteur normal
.
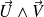On a donc obtenu :
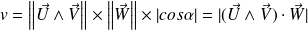
Trois vecteurs sont coplanaires si et seulement si leur produit mixte est nul.
En effet dans ce cas le parallélépipède est "dégénéré", son volume est nul.
Une autre propriété immédiate est que :
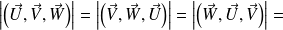
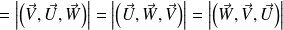
En effet le volume du parallélépipède ne dépend pas de l'ordre dans lequel on cite les vecteurs ! En revanche les 6 produits mixtes ne sont pas égaux, en effet le signe de
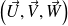est positif si le trièdre
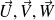est direct, il est négatif sinon. On obtient donc les égalités suivantes :
