Soient
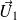et
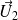deux vecteurs de
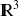, le produit vectoriel de
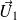par
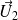est le vecteur défini par :
On admet les résultats suivants concernant la norme, la direction et l'orientation du produit vectoriel :
-
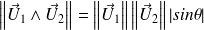où
est l'angle entre les vecteurs
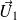et
. -
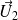Le vecteur
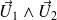est orthogonal à
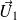et
. -
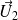L'orientation de
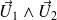est telle que le trièdre (
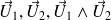) soit direct.
Il résulte de la propriété sur la norme du produit vectoriel que :
Deux vecteurs sont colinéaires si et seulement si leur produit vectoriel est nul.
Propriétés du produit vectoriel
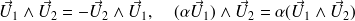
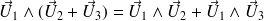
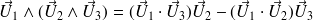
La norme du produit vectoriel de
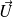par
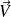est égale à l'aire du parallélogramme construit sur
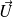et
.
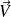Les deux propositions précédentes sont à démontrer en exercice.