Sauf mention contraire on se place dans
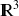muni d'un repère orthonormé
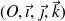Soient
,
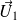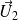et
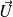des vecteurs de
,
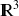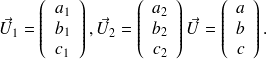
Le produit scalaire de
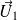par
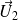est le réel défini par :
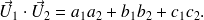
La norme (euclidienne) de
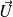est définie par :
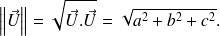
On a la relation qui lie le produit scalaire et les normes :
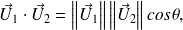
où
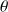est l'angle des vecteurs
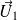et
.
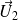Propriétés du produit scalaire
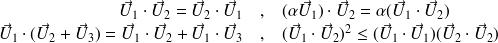
Proposition
Deux vecteurs sont orthogonaux si et seulement si leur produit scalaire est nul.