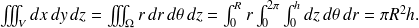Soit l'intégrale triple
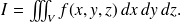
On suppose que le changement de variables
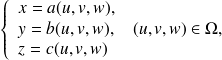
définit une bijection entre
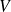et
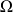(voir figure). On a l'équivalence
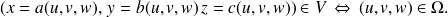
On peut définir une nouvelle fonction
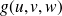par
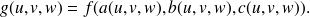
Par le changement de variables ci-dessus, on a
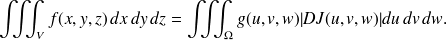
Le terme
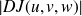représente bien la valeur absolue du jacobien, ce qui signifie que cette quantité ne dépend heureusement pas de l'ordre choisi pour les variables.
La démonstration repose sur une partition particulière du domaine
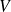en éléments qui sont les images par le changement de variables d'une partition de
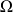en parallélépipèdes rectangles élémentaires (voir le document référencé).
La principale application du changement de variables dans les intégrales triples concerne les intégrales sur des cylindres ou sur des sphères. Par exemple, pour calculer le volume (bien connu ! ) d'un cylindre d'axe
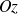, de rayon
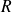et de "hauteur"
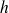, on utilise les coordonnées cylindriques et le domaine
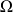correspondant est le parallélépipède rectangle
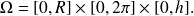
Le jacobien a été calculé dans un exemple précédent, il vaut
. D'où on retrouve le volume bien connu du cylindre :
