Soit le domaine
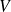de l'espace représenté sur la figure et considérons le domaine
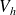constitué des parallélépipèdes rectangles
qui sont à l'intérieur de
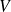. Il est clair que si
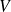est un parallélépipède rectangle, alors
.
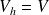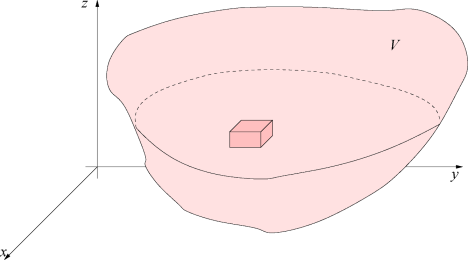
On définit alors pour
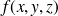donné, l'intégrale approchée
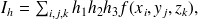
où
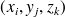est un point quelconque de
et où le triplet
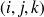parcourt un sous-ensemble de
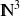tel que
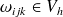. Chacun des éléments de cette somme représente la "masse" d'un parallélépipède rectangle élémentaire de masse volumique
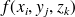. On a alors le résultat (non démontré) suivant
Quand
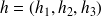tend vers
-
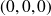
le domaine
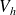"tend" vers
, -
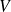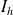tend vers le réel
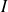, appelé l'intégrale triple de
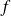
sur
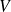et noté
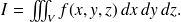
Comme on l'a déjà vu
-
Si
,
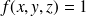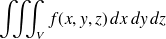est égal au volume de
. -
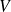Si
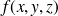est la masse volumique,
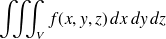est égal à la masse de
.
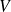On verra d'autres utilisations de l'intégrale triple plus loin.