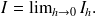Soit
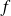 :
:
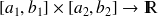 , on rappelle (voir Les intégrales doubles) que l'intégrale double de
, on rappelle (voir Les intégrales doubles) que l'intégrale double de
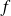 sur le rectangle
sur le rectangle
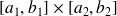 est construite par passage à la limite quand
est construite par passage à la limite quand
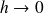 de
de
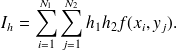
Dans cette expression, on a
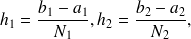
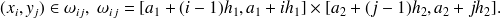
Soit
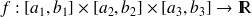 , on se propose de définir l'intégrale de
, on se propose de définir l'intégrale de
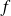 sur le parallélépipède rectangle
sur le parallélépipède rectangle
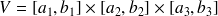 .
.
Dans le cas de l'intégrale double
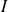 sur un domaine
sur un domaine
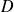 du plan, si
du plan, si
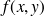 représente une masse surfacique alors
représente une masse surfacique alors
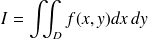 représente la masse de
représente la masse de
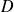 .
.
Pour l'intégrale triple, cette dernière interprétation reste valable. Si
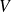 est un domaine de l'espace, si
est un domaine de l'espace, si
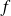 est la masse volumique, alors
est la masse volumique, alors
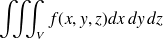 représente la masse de
représente la masse de
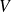 . Ceci est un exemple, les intégrales triples, comme on l'a évoqué, servent à faire bien d'autres calculs.
. Ceci est un exemple, les intégrales triples, comme on l'a évoqué, servent à faire bien d'autres calculs.
Soient
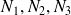 trois entiers donnés, soit
trois entiers donnés, soit
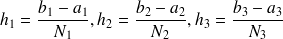
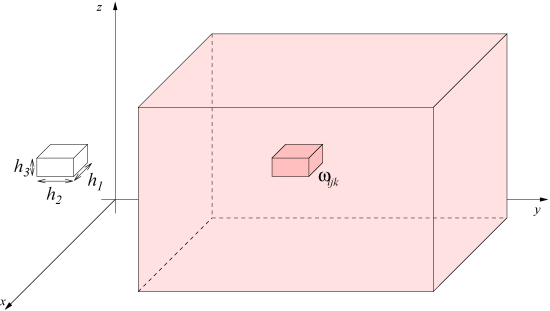
et effectuons (voir la figure "Découpage du parallélépipède rectangle") le découpage du parallélépipède en parallépipèdes élémentaires
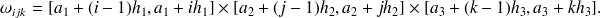
On définit alors
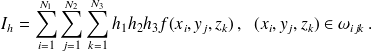
On appelle intégrale triple de
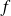 sur
sur
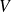 et on note
et on note
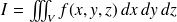
la limite