Soit l'intégrale double
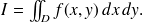
On suppose que par le changement de variables
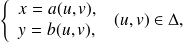
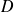est en bijection avec
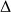, c'est à dire que l'on a l'équivalence
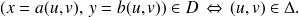
On définit une nouvelle fonction
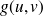par
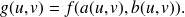
En reprenant les notations ci-dessus, on a
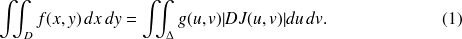
Le terme
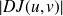représente la valeur absolue du jacobien. Ceci signifie que cette quantité ne dépend pas de l'ordre des variables contrairement au jacobien (vous pouvez en effet facilement vérifier que
).
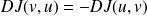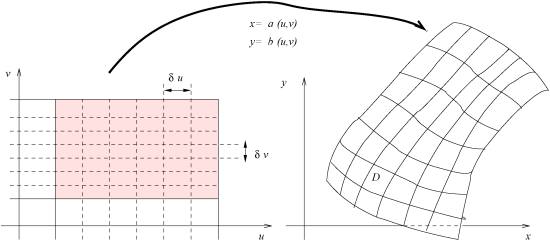
La démonstration repose sur une partition particulière du domaine
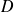en éléments qui sont les images par le changement de variables d'une partition de
en éléments rectangulaires, comme le montre la figure. L'image d'un élément de la partition de
peut être approchée par un parallélogramme dont l'aire est égale à (voir le document référencé)
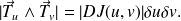
On peut comparer la formule \ref{chang} avec celle obtenue par changement de variables dans une intégrale simple. En effet soit la fonction
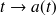bijective d'un intervalle
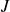sur un intervalle
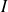. Alors
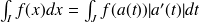
puisque si
est croissante la dérivée
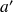est positive et les bornes de l'image de
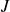sont croissantes. Par contre si
est décroissante la dérivée
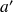est négative et les bornes de l'image de
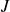sont décroissantes, d'où en inversant les bornes on fait apparaître
.
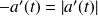La principale application du changement de variables dans les intégrales doubles concerne les intégrales sur des disques. Par exemple, pour calculer l'aire (bien connue ! ) d'un disque centré en
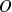et de rayon
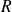, on "passe" en coordonnées polaires et le domaine
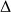correspondant est le rectangle
:
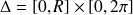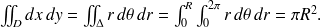
Le jacobien a été calculé dans le paragraphe référencé.