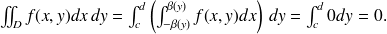Lorsque le domaine
 n'est pas un rectangle on peut refaire le raisonnement du paragraphe référencé et ramener le calcul de l'intégrale double à celui de deux intégrales simples. La difficulté consiste à trouver les "bonnes" bornes de ces intégrales simples. On peut montrer que
n'est pas un rectangle on peut refaire le raisonnement du paragraphe référencé et ramener le calcul de l'intégrale double à celui de deux intégrales simples. La difficulté consiste à trouver les "bonnes" bornes de ces intégrales simples. On peut montrer que
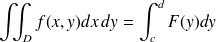
où
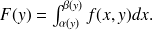
Le segment
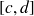 est la projection de
est la projection de
 sur l'axe
sur l'axe
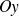 et le segment
et le segment
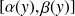 est la projection sur l'axe
est la projection sur l'axe
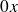 de l'intersection de
de l'intersection de
 avec la droite parallèle à l'axe
avec la droite parallèle à l'axe
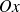 d'ordonnée
d'ordonnée
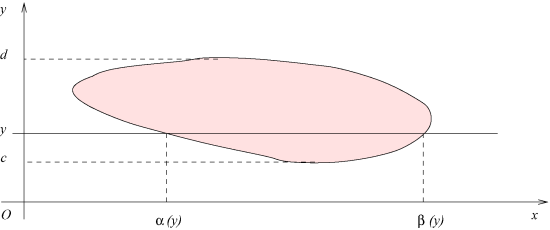
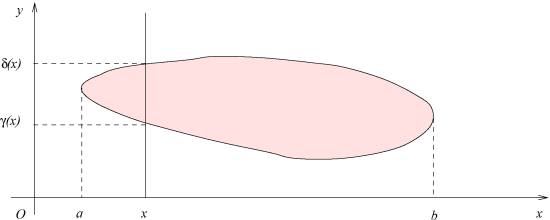
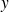 , comme le montre la figure. On peut dire aussi que les courbes
, comme le montre la figure. On peut dire aussi que les courbes
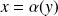 et
et
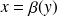 limitent respectivement le domaine
limitent respectivement le domaine
 "à gauche" et "à droite".
"à gauche" et "à droite".
Dans la formule on a commencé à intégrer
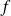 par rapport à
par rapport à
 avant de l'intégrer par rapport à
avant de l'intégrer par rapport à
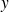 . On peut échanger les rôles de
. On peut échanger les rôles de
 et
et
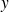 , ce qui donne :
, ce qui donne :
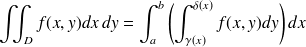
Le segment
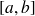 est la projection de
est la projection de
 sur l'axe
sur l'axe
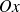 et le segment
et le segment
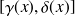 est la projection sur
est la projection sur
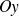 de l'intersection de
de l'intersection de
 avec la droite parallèle à l'axe
avec la droite parallèle à l'axe
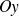 d'abscisse
d'abscisse
 comme le montre la figure. On peut dire aussi que les courbes
comme le montre la figure. On peut dire aussi que les courbes
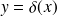 et
et
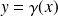 limitent respectivement le domaine "en haut" et "en bas".
limitent respectivement le domaine "en haut" et "en bas".
Si
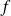 est une fonction impaire en
est une fonction impaire en
 , c'est à dire
, c'est à dire
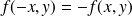 , si
, si
 est symétrique par rapport à la droite d'équation
est symétrique par rapport à la droite d'équation
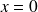 , c'est à dire
, c'est à dire
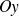 , alors
, alors
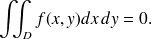
En effet, si le domaine
 est symétrique par rapport à
est symétrique par rapport à
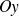 , cela signifie que
, cela signifie que
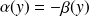 , faites une figure. Donc
, faites une figure. Donc