Soit le domaine
du plan représenté sur la figure et considérons le domaine
constitué des rectangles
qui sont à l'intérieur de
(voir figures pour des
différents). Il est clair que si
est un rectangle, alors
.
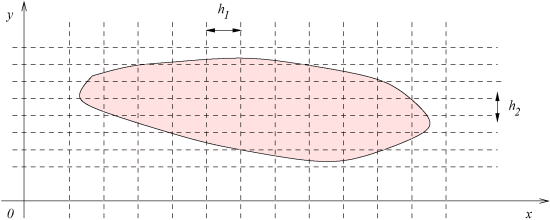
fig4[Zoom...]
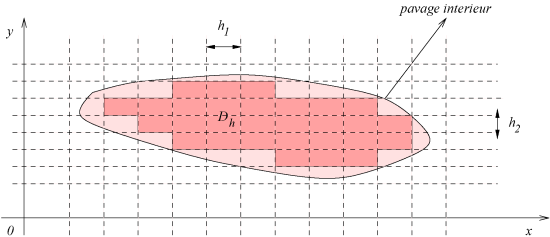
fig5[Zoom...]
fig6[Zoom...]
On définit alors une approximation de
par
où
est un point quelconque de
. Chacun des éléments de cette somme représente le "volume" d'un parallépipède rectangle dont l'aire de la base est
et dont la hauteur vaut
. On a alors le résultat (non démontré) suivant
Théorème
Quand
tend vers
-
le domaine
"tend" vers
, -
tend vers le réel
, appelé l'intégrale double de
sur
et notée
