On rappelle (voir chapitre 3) que l'intégrale d'une fonction
:
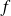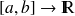sur le segment
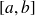est construite par passage à la limite quand
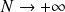de
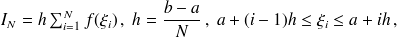
ou, ce qui est équivalent, par passage à la limite quand
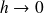de
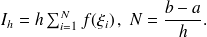
Soit
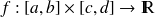, on se propose de définir l'intégrale de
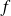sur le rectangle
.
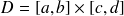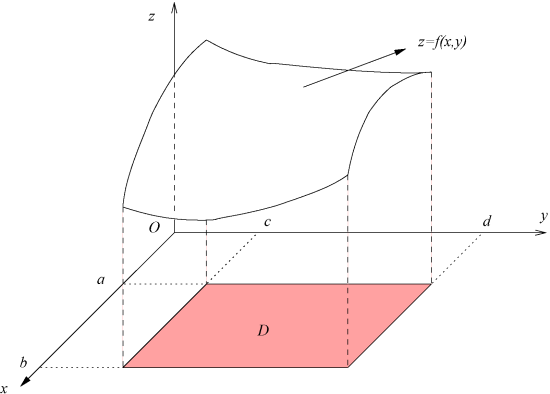
La construction de l'intégrale simple reposait sur le calcul d'une aire, celle de l'intégrale double est liée au calcul d'une mesure de volume (cela ne veut pas dire que toutes les intégrales doubles servent à calculer des volumes !).
Soient
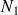et
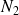deux entiers donnés, soit
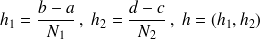
et effectuons (voir la figure) un découpage du rectangle en rectangles élémentaires
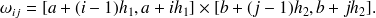
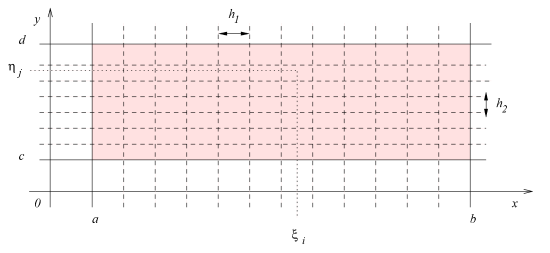
On définit alors
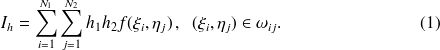
On appelle intégrale double de
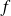sur
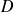et on note
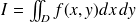
la limite
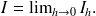
L'intégrale double représente la mesure du volume limité par les plans
,
,
,
,
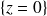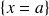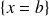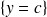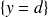et la surface d'équation
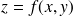, conformément à la figure
