On suppose que
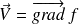, on a donc
,
,
.
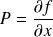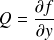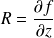La circulation du champ de vecteurs, définie dans le paragraphe référencé, vaut donc :
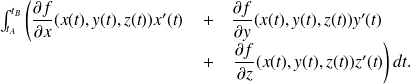
Si l'on note
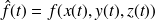, alors
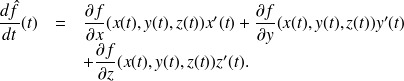
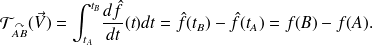
Donc on peut énoncer le résultat suivant :
Si le champ de vecteurs
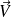dérive d'un potentiel
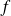alors la circulation de ce champ de vecteurs le long du segment curviligne
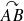est égale à
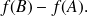
Une conséquence immédiate est :
-
Si le champ de vecteurs
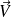dérive d'un potentiel, la circulation de ce champ de vecteurs le long du segment curviligne
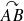ne dépend pas du chemin suivi pour aller de
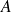à
. -
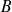La circulation d'un champ de vecteurs dérivant d'un potentiel, le long d'une courbe fermée est nulle.