Soit
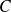 une courbe d'extrémités
une courbe d'extrémités
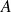 et
et
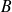 , soit
, soit
 une abscisse curviligne, soit (
une abscisse curviligne, soit (
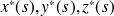 ) les coordonnées des points de
) les coordonnées des points de
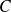 en fonction de
en fonction de
 et soit
et soit
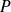 ,
,
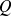 ,
,
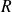 les composantes du champ de vecteurs
les composantes du champ de vecteurs
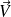 . Alors, par définition, la circulation
. Alors, par définition, la circulation
 du champ de vecteurs
du champ de vecteurs
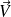 le long du segment curviligne
le long du segment curviligne
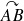 est égale à :
est égale à :

On peut démontrer que la circulation définie précédemment ne dépend pas du choix de l'abscisse curviligne. Par contre
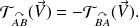
Souvent dans la pratique on ne connaît pas
 mais seulement une paramétrisation de
mais seulement une paramétrisation de
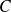 ,
,
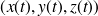 , on effectue alors un changement de variables dans l'intégrale qui définit la circulation, on a en effet :
, on effectue alors un changement de variables dans l'intégrale qui définit la circulation, on a en effet :
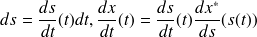 et des relations similaires pour
et des relations similaires pour
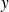 et
et
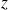 . On obtient :
. On obtient :
Si
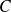 est une courbe d'extrémités
est une courbe d'extrémités
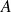 et
et
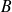 , paramétrée par
, paramétrée par
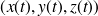 et si
et si
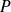 ,
,
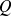 ,
,
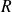 sont les composantes du champ de vecteurs
sont les composantes du champ de vecteurs
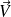 ,
,
alors la circulation du champ de vecteurs
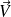 le long du segment curviligne
le long du segment curviligne
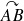 est égale à :
est égale à :
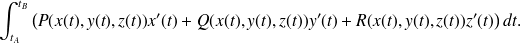
On peut garder pour la circulation la notation que l'on avait introduit pour le travail dans le paragraphe précédent, d'autres notations sont couramment utilisées.
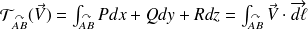 . Toutes ces expressions représentent la circulation du champ de vecteurs
. Toutes ces expressions représentent la circulation du champ de vecteurs
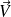 le long du segment curviligne
le long du segment curviligne
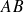 et se calculent par l'intégrale simple \ref {circulation}.
et se calculent par l'intégrale simple \ref {circulation}.