En ce qui concerne les équations à coefficients constants :

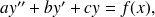
on peut trouver des solutions particulières pour certains seconds membres particuliers, dont voici les principaux.

1. Second membre de la forme 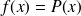, où 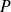est un polynôme : on cherche une solution particulière sous la forme d'un polynôme. Réfléchir au degré de ce polynôme selon que est nul ou non.

2. Second membre de la forme 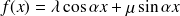. Il faut alors distinguer deux cas :

   • La fonction 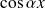(et donc 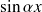) n'est pas solution de l'équation homogène. On peut alors chercher une solution particulière sous la forme

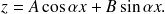
• La fonction 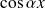(et donc 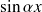) est solution de l'équation homogène. Il faut alors chercher une solution particulière sous la forme

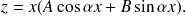
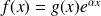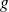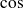3. Second membre de la forme , où est un polynôme ou une fonction en et , et 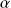un réel. La méthode générale consiste à faire le changement de fonction inconnue 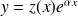et on se trouve ramené aux situations précédentes.