Dans ce paragraphe
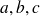sont des constantes.
On peut associer à l'équation
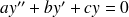
l'équation caractéristique :
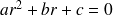
dont on note
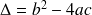, le discriminant. Les solutions réelles de
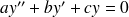dépendent du signe du discriminant :
-
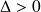: La solution générale de l'équation
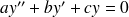est de la forme
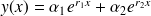
où
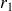et
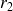sont les deux racines (réelles) de l'équation caractéristique
.
-
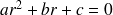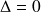: La solution générale de l'équation
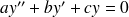est de la forme
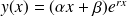
où
est la racine double de l'équation caractéristique
.
-
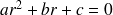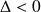: La solution générale réelle de l'équation
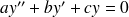est de la forme
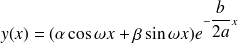où
.
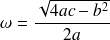La démonstration est à faire en exercices.
Les solutions complexes de
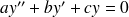sont données par le théorème plus général suivant :
La solution générale complexe de
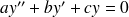est donnée par les deux cas suivants :
-
L'équation
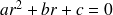admet deux racines
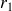et
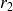distinctes dans
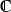alors on a
,
,
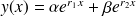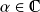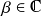
L'équation
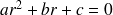admet une racine double
(réelle), alors on a
,
,
.
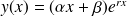
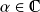
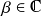