Comme on l'a vu dans le paragraphe référencé, la solution d'une équation différentielle n'est pas unique. On peut alors déterminer une courbe intégrale particulière en précisant un point 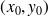par lequel elle doit passer. Ceci conduit à imposer une condition supplémentaire (souvent appelée condition initiale)

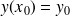
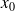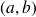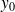où est donné dans et est donné dans .

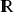Cette condition ne suffit pas toujours à assurer l'unicité de la solution comme le montre l'exemple suivant.

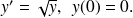
Il existe une solution évidente (laquelle ?). Cherchons maintenant une solution non identiquement nulle pour . Pour l'obtenir, on écrit

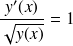
et on intègre des deux côtés par rapport à , ce qui donne (voir exercice)

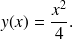
Tracer les deux courbes intégrales ainsi obtenues.