On appelle équation différentielle du premier ordre une équation de la forme
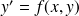
où
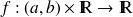 est donnée et où la fonction
est donnée et où la fonction
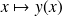 définie et dérivable de
définie et dérivable de
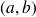 dans
dans
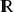 est l'inconnue. Une telle fonction
est l'inconnue. Une telle fonction
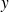 vérifiant
vérifiant
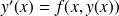
est appelée solution de l'équation différentielle.
En fait
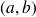 peut être
peut être
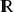 ou une partie de
ou une partie de
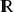 . Soit, par exemple, l'équation différentielle
. Soit, par exemple, l'équation différentielle
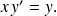
Elle admet les solutions
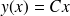 (le vérifier) définies sur
(le vérifier) définies sur
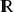 . Si,on la met sous la forme de la définition précédente :
. Si,on la met sous la forme de la définition précédente :
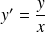
et elle n'est pas définie en
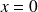 . Elle admet alors pour solutions
. Elle admet alors pour solutions
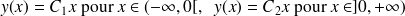
En fait l'écriture
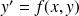 n'est pas nécessairement la forme sous laquelle apparait "naturellement'' l'équation différentielle.
n'est pas nécessairement la forme sous laquelle apparait "naturellement'' l'équation différentielle.
Un cas particulier très simple est la recherche des primitives
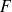 d'une fonction
d'une fonction
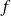 . En effet on résout alors
. En effet on résout alors
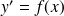
dont les solutions sont données par
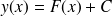
(
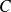 est le nom générique d'une constante quelconque). On remarque qu'il y a une infinité de solutions à l'équation différentielle
est le nom générique d'une constante quelconque). On remarque qu'il y a une infinité de solutions à l'équation différentielle
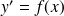 dépendant d'une constante arbitraire.
dépendant d'une constante arbitraire.
De manière générale, il y a une infinité de solutions à une équation différentielle du premier ordre. On appelle courbe intégrale ou courbe solution l'ensemble des points
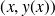 où
où
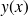 est une solution de l'équation différentielle. Il y a donc une infinité de courbes intégrales correspondant à une équation différentielle du premier ordre.
est une solution de l'équation différentielle. Il y a donc une infinité de courbes intégrales correspondant à une équation différentielle du premier ordre.