Définition
On dit que le champ de vecteurs
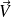dérive d'un potentiel vecteur, s'il existe un champ de vecteurs
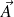deux fois continûment différentiable qui vérifie
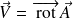
Attention
ne confondez pas le potentiel (scalaire) que l'on a défini précédemment et le potentiel vecteur que l'on définit maintenant.
Proposition
Une condition nécessaire et suffisante pour que le champ de vecteurs
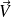dérive d'un potentiel vecteur
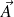est que
.
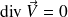Démonstration
On admettra que cette condition est suffisante, montrer en exercice que la condition est nécessaire.