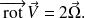On remarque bien sûr immédiatement le terme rotation dans le mot rotationnel. Quel est le lien ?
Soit
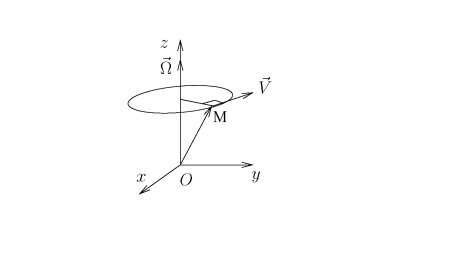
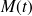un point d'un solide en rotation autour de l'axe
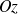à la vitesse angulaire
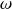. Cela signifie que si l'on note
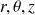les coordonnées cylindriques de
,
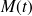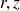sont constants et l'angle
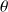varie en fonction du temps
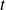, on a
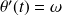. La position du point
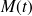est donc donnée par :
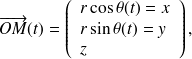
le champ de vecteurs vitesse, au point
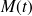est donné par :
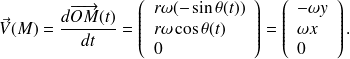
Si on note
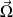le vecteur rotation instantanée, c'est à dire
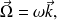
on retrouve le résultat connu liant le vecteur vitesse et le vecteur vitesse instantanée :
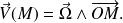
En introduisant le rotationnel, on trouve la relation supplémentaire :
