Définition
Soit
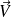un champ de vecteurs dont les composantes
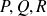sont des fonctions différentiable sur
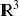, on dit que
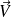est différentiable.
On appelle rotationnel de
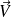et on note
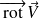, le champ de vecteurs dont les composantes sont données par :
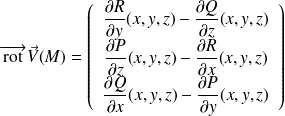
Proposition
Si
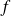est une fonction différentiable, si
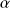est une constante, si
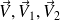sont des champs de vecteurs différentiables, on a les relations :
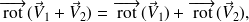
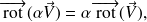
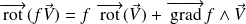
La démonstration de ces propriétés est l'objet de l'exercice proposé.