Si
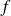est une fonction de
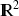dans
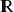différentiable, si le plan est muni d'un repère orthonormé
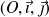, le vecteur gradient en
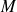est défini par :
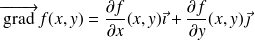
Si
et
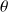sont les coordonnées polaires d'un point
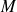de
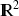, différent de
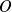, on définit une nouvelle base orthonormée du plan
:
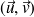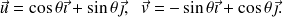
Si f est une fonction de
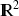dans
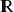, différentiable en
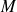, on définit la fonction
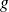par
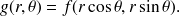On a alors l'expression du gradient suivante :
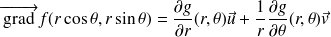
Cette proposition est démontrée en exercice de même que l'expression du gradient en coordonnées cylindriques :
Si
,
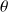et
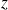sont les coordonnées cylindriques d'un point
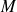de
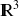n'appartenant pas à
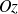, on définit les vecteurs
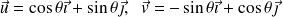
Si f est une fonction de
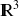dans
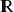, différentiable en
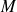, on définit la fonction
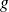par
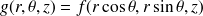. On a alors l'expression du gradient suivante :
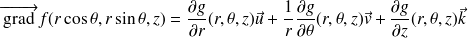
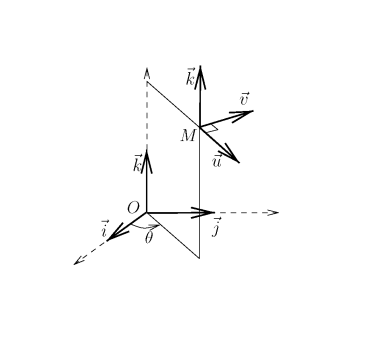
Voir une représentation des vecteurs
sur la figure.
On utilise les expressions précédentes si la fonction
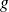est plus simple que
.
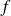