Définition
Soit
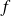une fonction de
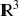dans
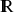différentiable, on appelle vecteur gradient de
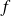et on note
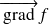, le champ de
vecteurs dont les composantes sont données par :
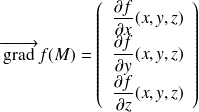, on note également
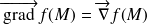
On a défini le vecteur gradient d'une fonction différentiable sur
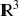, on pourrait bien sûr définir de façon similaire le gradient d'une fonction différentiable sur
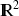et de façon plus générale sur
.
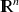Proposition
Si
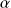est une constante réelle, si
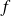et
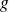sont deux fonctions différentiables, on a :
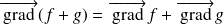
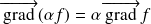
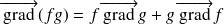
Les propriétés précédentes sont démontrées en exercice.