Visualisation de la multiplication modulo p
Dans cette appliquette, on visualise la multiplication de deux nombres
et
modulo
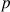. Les trois nombres,
peuvent être modifiés. On range la file des nombres
en cercle sur les sommets d'un polygone régulier. Le résultat de la multiplication
est visualisé, en partant de 0, en tournant
fois d'un arc correspondant à l'élément
. Chaque multiple de
est visualisé par un point noir.
On peut remarquer les choses suivantes:
Le nombre en bas à droite de la table est toujours 1. En d'autres termes,
, ce qui se démontre facilement en développant.À
fixé, l'ensemble des multiples
n'est égal à l'ensemble entier
uniquement quand
et
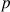sont premiers entre eux, c'est-à-dire n'ont pas de diviseurs communs. La colonne correspondante est alors une permutation de l'ensemble avec en particulier l'apparition de l'élément neutre
correspondant à l'inverse de
. On observe le phénomène contraire par exemple sur les horloges pour
,
et
: c'est le système des "trois huit" sur les chaînes de montages, avec des changements d'équipes de travailleurs à minuit, huit heure du matin et quatre heures de l'après-midi. Si le nombre d'heures dans la journée avait été premier, une telle organisation simple et régulière n'aurait pas été possible.
