Gestion d'un arbre binaire
Définition :
Avant de travailler sur les arbres binaires et arborescences en général, nous devons définir quelques notions et propriétés d'un arbre.
La figure ci-dessous permet de rendre explicite quelques propriétés définies sur un arbre. Certaines propriétés sont définies selon l'élément de référence de couleur bleu clair.
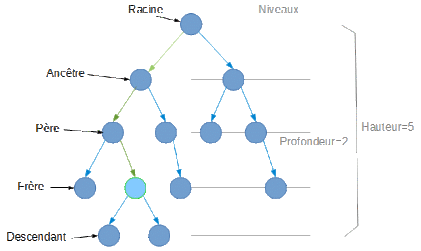
À cela, nous pouvons ajouter le nœud et la feuille. Le 1er désigne un élément de base de la structure d'arbre binaire, le 2e est un nœud sans fils (ni gauche ni droite). Toutefois, on pourra, par abus de langage, opposer le nœud et la feuille, le 1er n'ayant pas la propriété du 2e.
D'autres propriétés encore peuvent être définies :
Un arbre est vide, si aucune valeur n'est stockée dans l'arbre,
Un nœud est complet, s'il possède un fils gauche et un fils droit,
Un arbre est parfait, si toutes les feuilles de l'arbre sont au même niveau et tous les nœuds sont complets, etc.
Voici une liste non exhaustive des opérations de manipulation d'un arbre binaire :
Création d'un arbre,
Vérification de l'existence de l'arbre,
Accès à la racine de l'arbre,
Vérification de la nature d'un nœud,
Parcours et affichage des éléments,
Ajout d'un élément dans l'arbre,
Élimination d'un élément de l'arbre,
Calcul du nombre d'éléments d'un arbre,
Calcul de la hauteur de l'arbre,
Comparaison de 2 arbres,
Équilibrage d'un arbre.
Ces opérations nécessitent de travailler sur les composants de l'arbre, c'est-à-dire le nœud.
Les opérations sur les nœuds sont :
Modification ou accès au fils gauche,
Modification ou accès au fils droit,
Définition ou accès à la valeur,
Création du nœud,
Destruction du nœud.