TP 1 – Calcul de l'énergie d'interaction entre un acide aminé et une molécule d'eau.

Partie

Objectif : quantifier une interaction de type liaison hydrogène.

Avant-propos :

Nous utiliserons un logiciel open source de visualisation et d'édition de molécule, Avogadro. Ce TP n'est pas destiné à être un manuel bis du logiciel. L'objectif principal est ici de quantifier l'une des interactions moléculaires les plus importantes, l'interaction de type liaison hydrogène. Avant de vous lancer dans ce TP, il faudra installer le logiciel et se familiariser avec l'interface, notamment pour la construction des molécules et les calculs d'optimisation de géométrie. Pour cela, le site de l'éditeur, en anglais, est très bien illustré : http://avogadro.cc/

Question

Partie 1/ Construction d'un acide aminé – premier calcul de minimisation de l'énergie.

  1. Construire l'acide aminé L-thréonine dans sa forme neutre.

    Aide : Une structure de la L-thréonine est proposée avec le logiciel Avogadro. Ouvrir le menu Build > Insert > Fragment puis charger le composé L-serine.cml dans le sous répertoire amino-acid.

  2. Sélectionner le champs de force MMFF94. Calculer l'énergie de la structure non optimisée.

  3. Optimiser la structure de la molécule. Pour cela vous utiliserez d'abord 1000 pas de steepest descent suivi de 5000 pas de gradient conjugué.

  4. Calculer l'énergie de la structure optimisée.

Question 1 :

Comparer l'énergie avant et après optimisation de géométrie. Que pouvez-vous en dire ?

Solution détaillée

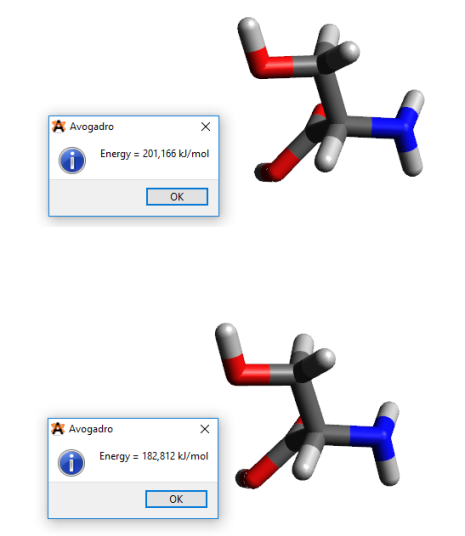
La figure 1 représente la structure de l'acide aminé avant et après optimisation. On remarque que la géométrie de la structure a été légèrement modifiée. L'énergie de la structure initiale (201,2 kJ/mol) est plus élevée que pour la structure optimisée (182,8 kJ/mol). C'est le principe même du calcul d'optimisation de géométrie : l'algorithme d'optimisation recherche un minimum sur la surface d'énergie potentielle.

Pour aller plus loin sur les méthodes de minimisation en modélisation moléculaire, reportez-vous au cours Unisciel :

http://uel.unisciel.fr/chimie/modelisation/modelisation_ch03/co/modelisation_ch03.html

Figure 1 : Structure de la L-théonine avant (en haut) et après (en bas) optimisation de géométrie. Les atomes d'hydrogène, de carbone, d'azote et d'oxygène sont respectivement en blanc, gris, bleu et rouge.
Remarque

En mécanique moléculaire, il existe de nombreux champs de force et les valeurs d'énergie sont dépendantes du champ de force utilisé. Pour plus d'information sur la notion de champs de force, se reporter au cours en ligne Unisciel :

http://uel.unisciel.fr/chimie/modelisation/modelisation_ch02/co/modelisation_ch02.html

Question

Partie 2/ Analyse d'une interaction acide aminé-molécule d'eau et quantification de l'énergie d'interaction.

  1. Construire une molécule d'eau. Optimiser sa structure et relever l'énergie de la molécule.

  2. Construire un système moléculaire dans lequel une molécule d'eau interagit avec l'acide aminé L-thréonine. Optimiser le système moléculaire. Relever l'énergie après optimisation.

Question 2 :

Quantifier l'énergie d'interaction entre la molécule d'eau et l'acide aminé. Est-ce une interaction de type liaison hydrogène ?

Solution détaillée

Pour estimer l'énergie d'interaction acide aminé-molécule d'eau (que l'on notera ΔE), on peut considérer en première approximation que :

ΔE = Ecpx - EThr - EH2O

avec :

  • Ecpx l'énergie du système L-thréonine – H2O optimisée

  • EThr l'énergie de l'acide aminé optimisé dans la partie 1

  • EH2O l'énergie de la molécule d'eau.

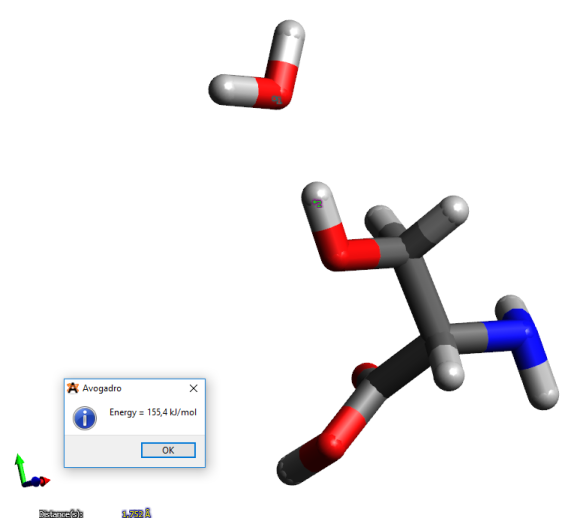
D'après cette formule, ΔE = 155,4 - 188,812 - 0 = -33,412 kJ.mol-1

Figure 2 : Structure du complexe L-thréonine – H20 après optimisation de géométrie.
Explication

Plusieurs choses sont à noter :

  • En mécanique moléculaire, l'énergie d'une molécule d'eau dans le vide est nulle. Lors de l'optimisation de géométrie de la molécule d'eau, les seules variables sont les deux distances O-H et l'angle HOH. Dans un champ de force classique, seuls les termes Énergie de liaison et Énergie d'angle ont une influence sur l'énergie de la molécule d'eau. Puisque par définition chacun de ces termes représente une énergie de déformation par rapport à une structure idéale, ils sont nuls pour la molécule d'eau optimisée dans le vide.

  • Dans cet exemple, l'énergie d'interaction est négative. Cela correspond donc bien à une interaction favorable (stabilisante) entre les deux molécules.

  • Dans cet exemple, la distance entre l'atome d'hydrogène et d'oxygène est d'environ 1,7 Å. Sachant que l'énergie d'interaction est d'environ 30 kJ/mol et que l'angle formé par les atomes impliqués dans l'interaction est d'environ 176°. Il s'agit donc bien d'une interaction de type liaison hydrogène.

Attention toutefois, plusieurs autres paramètres influent sur l'énergie de l'interaction comme le type d'atome donneur de la liaison hydrogène, la distance et l'angle de la liaison hydrogène, ...

Remarque

Il semble que le champs de force MMFF94 surestime légèrement l'énergie d'interaction. Ci-dessous, l'ordre de grandeur d'une liaison hydrogène en fonction de l'atome accepteur :

ΔE(H...F) = -30 kJ/mol

ΔE(H...O) = -20 kJ/mol

ΔE(H...N) = -10 kJ/mol

Fondamental

En conclusion, il faut donc retenir qu'une liaison hydrogène typique est de l'ordre de quelques dizaines de kJ/mol.

Question

Question 3 :

On s'intéresse à une réaction d'association entre un récepteur (R) et un ligand (L) formant un complexe ligand-récepteur-ligand (RL) tel que : R + L = RL

En supposant que l'association soit uniquement due à une interaction de type liaison hydrogène, quelle est la constante d'association et de dissociation de cet équilibre à 25°C ?

Solution détaillée

En première approximation on pourra considérer que l'enthalpie libre d'association (ΔG) est équivalent à l'énergie d'association tel que nous l'avons mesuré :

ΔG ≈ ΔE ≈ -30 kJ/mol

Sachant que pour la réaction R + L = RL :

  • \(\Delta G = G_{RL} - \left( G_R + G_L \right) = -R \cdot T \cdot ln(Ka)\)

  • \(Ka = e^{ - \frac{\Delta G}{RT}}\)

  • \(Kd = \frac{1}{Ka}\)

On peut calculer \(Ka \approx 1,8 \cdot 10^{5}\) et \(Kd \approx 5,5 \cdot 10^{-6}\)

Fondamental

En d'autres termes, une interaction de type liaison hydrogène « équivaut » à une affinité de liaison de l'ordre du micromolaire (µM).