Nombres entiers relatifs
L'étape suivante consiste à représenter sous forme binaire les nombres entiers relatifs. L'idée immédiate mais naïve consiste à consacrer le bit d'extrême gauche comme bit de signe, 0 pour les nombres positifs et 1 pour les négatifs : avec 9 bits, par exemple, on représente les entiers compris entre -255 et +255. Mais le nombre 0 est représenté deux fois, 0 0000 0000 (+0) et 1 0000 0000 (-0) et surtout la somme de deux nombres opposés n'est pas nulle ce qui est gênant. Ainsi, si on effectue 214 + (-214), on obtient :

Qui est visiblement non nul !
Pour effectuer cette somme, on procède colonne par colonne comme en base 10. Chaque colonne ou étage est susceptible de générer un report ou retenue pour l'étage suivant selon la règle simple suivante : 0+0=0 pas de report, 0+1=1+0=1 pas de report, 1+1=0 avec un report à 1 et enfin, 1+1+1=1 et un report (le dernier 1 de la somme provient du report de l'étage précédent).
Pour résoudre le problème, on définit le complément à 2 d'un entier positif qui représente son opposé de manière à ce que la somme de deux entiers opposés soit bien égale à 0. Pour obtenir le complément à 2, il suffit de retenir la recette qui est très simple et qui se déroule en deux étapes vraiment élémentaires. La première étape consiste à complémenter chaque bit du nombre entier positif auquel on a ajouté le bit de signe à 0 comme dans la méthode naïve : cela signifie qu'un bit à 0 passe à 1 et un bit à 1 passe à zéro. On obtient ainsi le complément à 1. Puis, la seconde étape consiste à ajouter le nombre 1 au complément à 1. On obtient alors le complément à 2. Si on reprend l'exemple précédent :
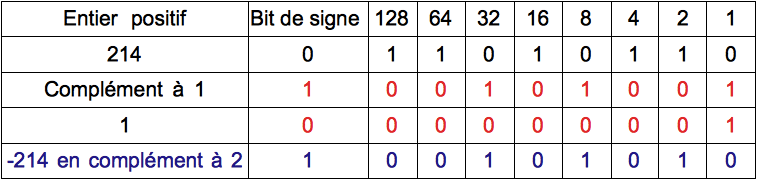
La dernière ligne, -214 en complément à 2 est obtenue en sommant les deux lignes rouges, le complément à 1 et +1. Si on somme à présent les deux entiers opposés, soit 214 + (-214), on obtient :
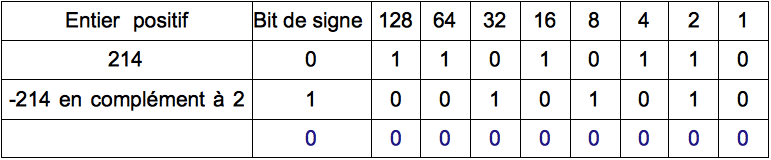
Certes, il y a un dernier report qui passe dans un dixième bit, mais sur 9 bits, la somme de deux entiers opposés est bel et bien nulle.





